
こんにちは。
今回はコイル、コンデンサの電流、電圧の進み、遅れの覚え方を紹介します。
コイル、コンデンサの抵抗の表し方
最初に、コイルとコンデンサーの交流回路上での抵抗の表し方を覚えましょう。
コイルのインダクタンスをL(ヘンリー)とすると、交流回路におけるコイルの抵抗は、j ωL になります。
コンデンサの静電容量C(ファラド)とすると、交流回路におけるコンデンサーの抵抗は、1/jωCになります。
jは虚数と言って、j=ルート(-1)となり、j*j = -1となります。実数ではないものです。
このまま覚えて下さい。
複素平面
交流回路では、j(虚数)を扱うことになります。
そこで、実数と虚数を含めた平面を複素平面と言います。縦軸に虚数、横軸に実数をとります。
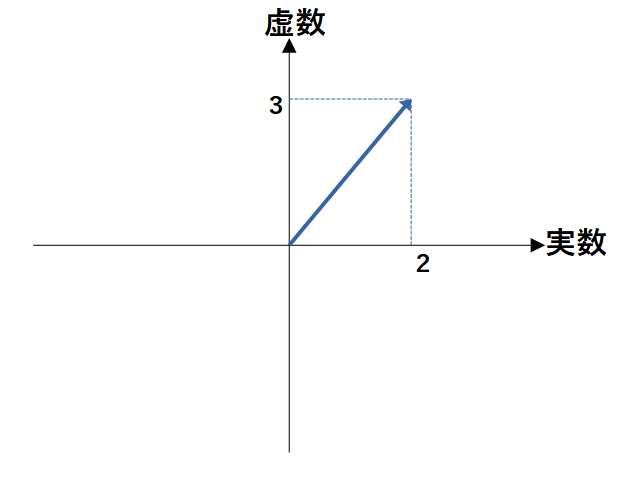
例えば、a = 2 + 3 jという複素数を複素平面で表すと、下の矢印になります。
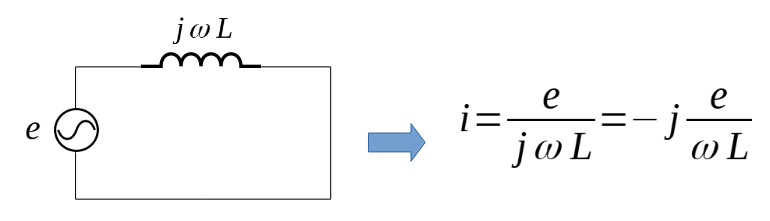
コイルの場合
交流電源eとインダクタンスLのコイルを直列で接続した場合の電流の値は下記の様になります。
ここで、電流を複素平面で表してみると、虚数のみに矢印が向きます。
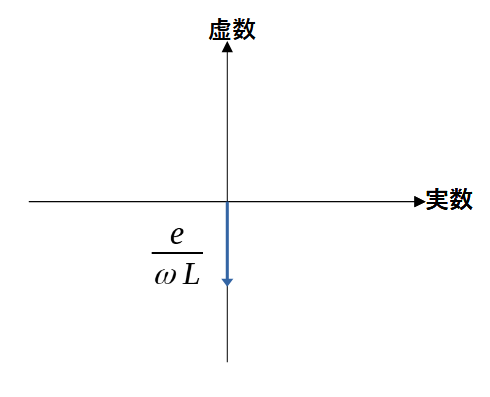
この時、矢印の角度は下に90度向いているので、90度遅れていることになり、電流は電圧に対して90度の位相が遅れていることになります。
コンデンサの場合
交流電源eと静電容量Cのコンデンサを直列で接続した場合の電流の値は下記の様になります。
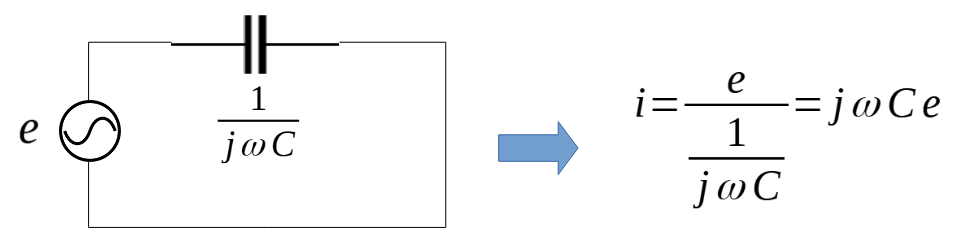
先ほどと同様に、電流を複素平面で表してみると、虚数のみに矢印が向きます。
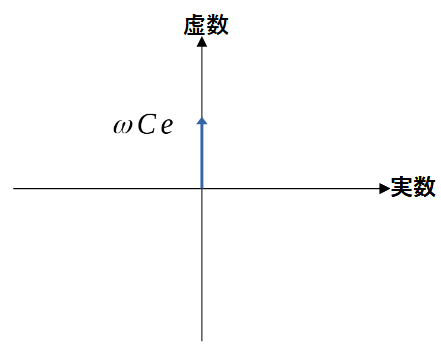
この時、矢印の角度は上に90度向いているので、90度進んでいることになり、電流は電圧に対して90度の位相が進んでいることになります
まとめ、複素平面で進み、遅れが分かる
上記のように、複素平面で表すと、進み、遅れが視覚的に分かります。
最初は慣れないかもしれませんが、複素平面でベクトル図を描いていくと、抵抗、コイル、コンデンサが含まれた回路でも、簡単に電流、電圧を求められ、進み、遅れも理解してくるようになってきます。
簡単な問題から、一度、複素平面で解いてみてはいかがでしょうか。

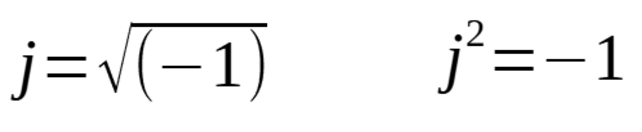
コメント